การให้เหตุผลแบบนิรนัย

การให้เหตุผลแบบนิรนัยเป็นวิธีการให้เหตุผลโดยสรุปผลจากข้อความซึ่งเป็นความจริงทั่วไปมาเป็นข้ออ้างเพื่อสนับสนุนให้เกิดข้อสรุปที่เป็นความรู้ใหม่ที่เป็นข้อสรุปส่วนย่อยข้อสรุปที่ได้จากการให้เหตุผล... อ่านเพิมเติม

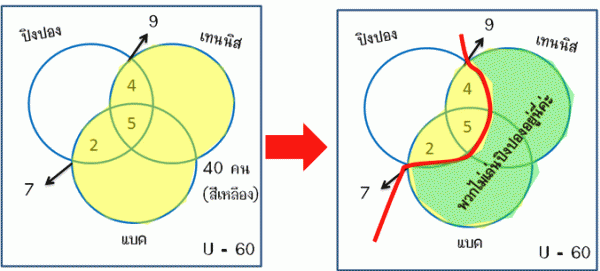
ยูเนียน อินเตอร์เซกชัน และคอมพลีเมนต์ของเซต

ยูเนียน อินเตอร์เซกชัน และคอมพลีเมนต์ของเซต เป็นส่วนหนึ่งของการกระทำระหว่างเซต เรานิยมเขียนออกมาในสองรูปแบบด้วยกันคือแบบสมการ และแผนภาพเวนน์-ออยเลอร์ เราลองมาดูกันครับว่ายูเนียน อินเตอร์เซกชัน และคอมพลีเมนต์ของเซต...อ่านเพิ่มเติม

สับเซตและเพาเวอร์เซต

ถ้าสมาชิกทุกตัวของ A เป็นสมาชิกของ B แล้ว จะเรียกว่า A เป็นสับเซตของ B จะเขียนว่า
เซต A เป็นสับเซตของเซต B แทนด้วย A ⊂ B

ถ้าสมาชิกบางตัวของ A ไม่เป็นสมาชิกของ B จะเรียกว่า A ไม่เป็นสับเซตของ B
เซต A ไม่เป็นสับเซตของเซต B แทนด้วย A ⊄ B...อ่านเพิ่มเติม

เอกภพสัมพัทธ์

เซตว่าง และเอกภพสัมพัทธ์ จากบทเรียนเรื่องเซต คณิตศาสตร์ ม.4 ถือเป็นพื้นฐานของเรื่องเซต ที่เราควรจะทำความสนิทสนมกับมันให้มาก เพราะมันเป็นพื้นฐานทั้งหมดในการเรียนเรื่องเซต...อ่านเพิ่มเติม

ค่าสัมบูรณ์ของจำนวนจริง

ค่าสมบูรณ์ของจำวนจริง a : เมื่อกำหนดให้ a เป็นจำนวนจริงระยะจากจุด 0 ถึงจุดที่แทนที่จำนวนจริง a เขียนแทนด้วย |a|
เช่น |2| หมายถึง ระยะจากจุด 0 ถึงจุดที่แทนจำนวน 2 ซึ่งเท่ากับ 2 หน่วย
|-2| หมายถึง ระยะจุด 0 ถึงจุดที่แทนจำนวน -2 ซึ่งเท่ากับ 2 หน่วย...อ่านเพิ่มเติม

สมบัติการไม่เท่ากัน

สมบัติการไม่เท่ากันของจำนวนจริง

สมบัติเกี่ยวกับการไม่เท่ากันของจำนวนจริง มีดังนี้ ( ให้ a , b , c , d ∈ R )

การไม่เท่ากันของจำนวนจริง ไม่มีสมบัติการสะท้อน ไม่มีสมบัติการสมมาตร แต่มีสมบัติอื่นดังนี้...อ่านเพิ่มเติม

สมบัติของจำนวนจริงเกี่ยวกับการบวกและการคูณ

ในระบบจำนวนจริง มีเอกลักษณ์การบวกจำนวนเดียวคือ 0 เมื่อ  a เป็นจำนวนจริงใดๆ a+0 = a = 0+a

ในระบบจำนวนจริง อินเวอร์สการบวกของจำนวนจริง a หมายถึง จำนวนจริงที่บวก a แล้วได้ผลลัพธ์เป็น 0 ใช้สัญลักษณ์ “-a” แทนอินเวอร์สการบวกของจำนวนจริง  a...อ่านเพิ่มเติม

จำนวนจริง

จากแผนผังแสดงความสัมพันธ์ของจำนวนข้างต้น จะพบว่า ระบบจำนวนจริง จะประกอบไปด้วย...อ่านเพิ่มเติม

การให้เหตุผล

การตรวจสอบว่าข้อสรุปสมเหตุสมผลหรือไม่นั้นสามารถตรวจสอบได้หลายวิธี เช่น การวาดแผนภาพ
- ถ้าแผนภาพที่วาดกรณีที่เป็นไปได้ทุกกรณีแสดงผลตามที่กำหนด จึงกล่าวว่าการสรุปผลสมเหตุสมผล
- แต่ถ้ามีแผนภาพที่ไม่แสดงผลตามที่สรุปไว้ การสรุปผลนั้นไม่สมเหตุสมผล

เซต

เซต เป็นคำใหม่ที่เราจะรู้จักตอนเรียน ม.4 ซึ่งจริง ๆ แล้ว เซต ก็คือ การบอกลักษณะที่เป็นกลุ่มของอะไรสักอย่าง เช่น เซตของจำนวนเฉพาะ หมายถึง กลุ่มของจำนวนเฉพาะ ดังนั้น สิ่งที่อยู่ในเซตนี้จะต้องเป็นจำนวนเฉพาะเท่านั้น เช่น...อ่านเพิ่มเติม